 INTRO: For those interested in headphone amps, gain is an important topic. Here are the essentials about gain with lots of links to more information. In addition to this introduction explaining gain, there are later sections on:
INTRO: For those interested in headphone amps, gain is an important topic. Here are the essentials about gain with lots of links to more information. In addition to this introduction explaining gain, there are later sections on:
RELATED ARTICLES: The following may be useful understanding how gain fits into the bigger picture:
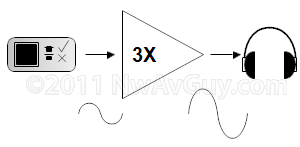
WHAT IS GAIN? Put simply, gain is the maximum amount an amplifier can increase a signal. In the world of headphones, it's usually voltage gain. The diagram above shows a source with a weak output made 3 times stronger by an amplifier. Applying gain to a signal doesn’t normally change the dynamic range, it just makes everything louder. Other ways to specify gain, such as power and current, are rarely used for headphone gear.
YACA (Yet Another Car Analogy): The relationship between gain, volume, and maximum power can be confusing to some. Using car analogies might help:
- Gain Is Like The Gear Selection - When a car is in its lowest gear its top speed is limited to a fairly low value but it can climb steep hills. It's somewhat the same with a headphone amp set to low gain. Think of a gain switch as 1st, 2nd, and 3rd gear on a car's transmission. Different gears are used for different driving conditions.
- Volume is like the Throttle (Accelerator) - The volume control adjusts the overall power to the headphones much like the throttle in a car adjusts the power to the wheels.
- Maximum Power is like Top Speed - Most cars are capable of going faster than most people need. While a car might have a top speed of 100 MPH, in first gear, it might only do 40 MPH. So gain can be used as a way to limit maximum output and better match the output to a given pair of headphones. The difference between the top speed and the highest speed limit is somewhat analogous to excess gain.
WHY DOES GAIN MATTER? If you don't have enough gain, your headphones probably won’t get loud enough. If you have too much gain, you will be forced to use only a small portion of the volume control's range, there may be increased channel balance problems, more noise, more distortion, and you could even damage your headphones more easily. Most any amp will perform worse at higher gain settings so you want to use the least amount of gain that gets the job done.
GAIN AND VOLUME ARE IMPLEMENTED DIFFERENTLY: Turning down the volume is not the same as lowering the maximum gain (with a few rare exceptions). A race car doesn't turn into a family car if you never use more than half throttle. Certain compromises were made in the race car that make it less suitable for family car duty even if you try to drive it slowly. The same is true with a high gain amp. It's important to not have much more gain than you really need.
GAIN CAN BE USED TO LIMIT MAXIMUM POWER: If you have some fairly efficient headphones that are as loud as you would ever want with only 0.7 volts of audio. But you have a high-end desktop headphone amp that can put out 10 times as much (7 volts). By reducing the gain, even if you accidentally turn the volume all the way up, you can limit the maximum power to your headphones. This can help prevent hearing damage and even headphone damage. It also also allows using much more of the volume control's range making volume adjustments easier and more accurate.
GAIN CAN CHANGE WITH DIFFERENT HEADPHONE LOADS: If an amp doesn’t have an output impedance below 2 ohms the gain will change with different loads. The higher the output impedance, the more dramatic the change. For example, an amp with a 120 ohm output impedance with 5X gain at no load, will have only 3.5X gain with 300 ohm headphones and only 0.6X gain with 16 ohm headphones. This is another reason it’s important to know the output impedance.
GAIN CANNOT CORRECT FOR A LACK OF MAXIMUM POWER: If your headphones need 5 volts but your amp is only good for 2 volts cranking up the gain won't help any and will just make the amp clip sooner. Clipping is what happens when an amp runs out of power. The rest of this article assumes your amp is capable of enough power for your headphones. For more on this topic see: More Power?
GAIN DETAILS
HOW IS GAIN EXPRESSED? Gain is usually expressed as a factor (ratio), such as 4X, or in decibels (dB) such as 12 dB. In this case, 4X is the same as 12 dB and simply means with the volume control set to maximum, the output voltage of the amplifier will be four times higher than the input voltage. If you put 1 volt in you will get 4 volts out (assuming you don't exceed the maximum output capability). I show how to convert from ratios to dB and back in the Gain Calculations section below.
WHAT ARE TYPICAL GAINS? Headphone amps that have just a single fixed gain typically range from 2X (6 dB) to 5X (14 dB). For amps with two gain settings, low gain might be 2X to 3X and high gain 5X to 8X. Some amps have three or more gain options while others allow changing internal jumpers or resistors to set the gain.
A ROUGH GUIDELINE: If you want to skip the more technical details, the table below offers some idea of what gain will be usable with various headphones and sources:
| Headphones | Portable | USB DAC | HOME | < Source |
| IEM 100 - 115 dB/mW 16 - 32 ohms | 1X/0 dB | 1X/0 dB | 1X/0 dB | |
| Sensitive Low Impedance Full Size Grado, Denon, Etc. | 2X/6 dB | 1X/0 dB | 1X/0 dB | |
| Average Full Size HD5xx/600/650 100 - 300 ohm | 5X/14 dB | 3X/10 dB | 2X/6 dB | |
| High Impedance Full size 300 - 600 ohm | 10X/20 dB | 5X/14 dB | 3X/10 dB |
DO I NEED AN AMP AT ALL? If your headphones already get plenty loud enough, and you're happy with the sound, odds are you don't need an amp. But if they don't get loud enough, an amp may be required. The table above shows several combinations where the gain is listed as 1X which implies no amp is required. But you might still want to use an amp to lower the output impedance of your source. For example, the iPod Touch 3G has a 7 ohm output impedance. With balanced armature IEM headphones this causes audible problems. See: Output Impedance. So while the IEMs don't need any more voltage they can still benefit from a lower output impedance. Some amps, like the O2, can be easily configured for 1X gain and improve the sound of higher impedance sources. For more on headphone amps in general, see: Headphone Amps Explained
EXCESS GAIN
EXCESS GAIN: If your amp has just enough gain for your headphones to hit the desired level at full volume with a 0 dBFS signal it's sort of like having a car with a top speed equal to the highest speed limit in your area. There might be times when you want to go even faster. But how much extra do you need? The amount of volume control range above where a 0 dBFS signal clips is considered “excess gain”. Here are some points to consider:
- Excess Gain Is A Tradeoff - As described above in Why Does Gain Matter, too much gain has negative side effects. So it's a tradeoff between those side effects and how much excess gain you want.
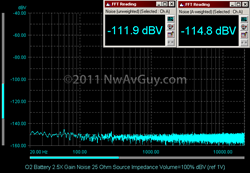
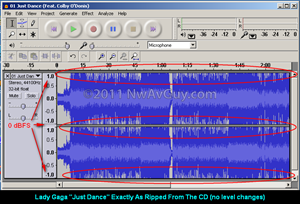
- Excess Gain Is Only Useful For Quiet Tracks - Most properly recorded digital music is designed to hit, or get within 1 dB of, 0 dBFS. If your amp has excess gain, using full volume with normal tracks will cause the amp to clip (badly distort) and may even damage your headphones. But, without excess gain, rare quiet tracks may not be loud enough even with the volume at 100%. One solution is having a reasonable amount of excess gain. Another solution is to normalize quiet tracks to 0 dBFS using Audacity or other software. This simply raises the levels so the loudest portion of the track is at 0 dBFS. Yet another solution is to use ReplayGain which helps equalize all tracks to roughly the same perceived volume.
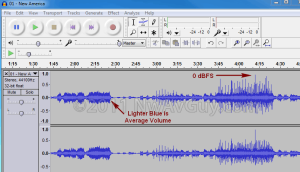
- ReplayGain (volume leveling) - If you use something like ReplayGain nearly all of your music should play at a consistent subjective level. ReplayGain is essentially like having someone automatically adjust the volume for each track (or CD). The default target loudness of 89 dB leaves 14 dB of headroom between the average volume and 0 dBFS. For the most compressed pop music this means the peak levels will be as much as 6 dB below 0 dBFS, while dynamic music will get much closer to, or even hit, 0 dBFS. If you use ReplayGain, or something similar, for volume leveling, you may want up to 6 dB of excess gain to allow for the overall volume reduction ReplayGain applies to some tracks. For more on average volume see: More Power?
- Dynamic Range – It’s important to note that neither the gain of an amplifier, nor ReplayGain, normally changes the dynamic range of music. Gain changes normally apply equally to the softest and loudest portions of the signal (music). To change the dynamic range you have to apply compression, limiting, (or dynamic range expansion).
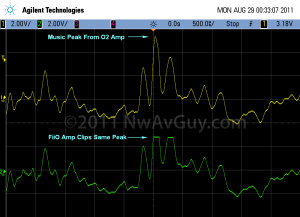
- Clipping vs Maximum SPL – Some amps have plenty of power and your headphones, or ears, will give up before the amp does when dialing up excess gain on a recording that already hits 0 dBFS. But, in some circumstances (especially with low sensitivity headphones), the amp might run out of power first. If you want to be assured your amp will never clip, just work backwards from the amp’s maximum output into your headphone impedance to determine the gain. If your amp maxes out at 7 volts, and your source is 2 volts, set the gain to 3.5X and the amp will never clip even at full volume with a worst case recording. See: More Power?
- 9 dB Excess Gain Is A Reasonable Maximum - I would aim for at least 3 dB of extra gain but somewhere around 9 dB the negative side effects already mentioned start to outweigh the advantages. A few might want to go as high as 12 dB but only if they've used something like ReplayGain to normalize their music library to a lower than normal average volume or have other unusual requirements.
- The Math – 3 dB of extra gain means multiplying the minimum gain by 1.4 and for 6 dB multiply by 2, and for 9 dB multiply by 2.8.
THE CHANNEL BALANCE PROBLEM: Devices with conventional volume controls may have audible channel imbalance at very low volumes. It's extremely difficult to manufacture volume control potentiometers that maintain tight channel balance below about -40 dB (referenced to full volume). Having too much excess gain forces using only the lower portion of the volume control's range with normal recordings. If your amp has 10 dB of excess gain, for example, -40 dB below 0 dBFS on the volume control is -50 dB below full volume. The channel balance error will likely be much greater and more audible. Some products get around this problem by using digitally controlled electronic volume controls that can maintain better channel balance at low settings but these can add distortion and often controlled by up/down buttons rather than a simple knob. Stepped precision attenuators are another solution but are expensive and sometimes their step size is too great.
GAIN CALCULATIONS
HOW DO YOU CONVERT FROM Gain Ratio X TO dB? The math requires using a function known as base 10 logarithm (LOG on a calculator). But you can also just use an online dB calculator:
- Online dB Calculator
- Gain in dB = 20 * LOG10 ( Gain Factor ) [i.e. 20 * LOG10 ( 4 ) = 12 dB]
- Gain Factor = ANTILOG10 ( Gain in dB / 20 ) [i.e. ANTILOG10 ( 12 / 20 ) = 4X]
HOW MUCH GAIN DO I NEED? This comes down to only three things:
- How much voltage your headphones need
- How much output your source has
- How much excess gain you want.
HEADPHONE REQUIREMENTS: For a given pair of headphones, the More Power? article helps determine what your headphones need. This is related to the sensitivity and impedance of your headphones which vary widely. The most efficient IEMs only need about 0.1 volts to play loudly, Sennheiser HD600s need about 2.3 volts and Beyer DT880-600s need about 6 volts or 60 times more than the IEMs.
SOURCE OUTPUT LEVEL: Sources have a maximum output level. It's the output voltage at 0 dBFS (the loudest digital music can get) and at full volume (if the source has a volume control). Sources can be roughly divided into the follow categories (all voltages are Vrms):
- Portable Players - Most of these have a maximum output of 0.5 - 1.0 volts from either their headphone jacks or LOD (Line Output Dock) connectors. The iPod Touch is 0.5 volts from the LOD.
- USB Powered DACs - Most of these have a maximum output of 1.5 volts or less.
- Normal Home Audio Gear - The Redbook standard for any home equipment that plays digital audio is 2 volts. Some go slightly higher up to 2.5 volts. There are also a few USB powered DACs that can manage similar voltages (such as the HRT Music Streamer II).
- Unusual (rare) Home Sources - A few companies, arguably unwisely, have decided to go well above the established standard and output more than 2.5 volts. But I'm not aware of any that go above 3.3 volts unless they have a volume control.
- Balanced Outputs - These can be misleading because balanced outputs normally have twice the output of unbalanced outputs. A 4 volt balanced output, used with an unbalanced adapter or cable, is really only 2 volts.
- Unknown Sources – See DIY Gain Measurements below.
CALCULATING THE REQUIRED GAIN: Once you've figured out the above three requirements, it's fairly easy to calculate the gain you need. Just follow these steps (examples are given for the HD600's driven from an iPod LOD with 3 dB excess gain):
- Calculate Minimum Gain: Gain Factor = Vout / Vin [i.e. 2.3Vout with 0.5V Vin = 2.3/0.5 = 4.6X]
- Convert To dB: Minimum Gain in dB = 20*LOG( Gain Factor ) [i.e. 20*LOG(4.6) = 13.2 dB]
- Add Excess Gain: Final Gain in dB = Minimum Gain + Excess Gain [i.e. 13.2 + 3 = 16.2 dB]
- The result is 16.2 dB (6.5X) of gain for the example case.
- You can also multiply 4.6X by 1.4 to get 6.5X (1.4 is 3 dB excess gain as a ratio)
- If you know the output impedance multiply by (Zload + Zout) / Zload
INPUT OVERLOAD: Also be aware that many devices, especially portable ones, have inputs that can be overloaded by certain sources. Because the Redbook standard is 2 volts, a lot of devices are designed to only handle about 2.1 volts such as the FiiO E9 desktop amp. And the portable FiiO E7 overloads at about 1.2 volts on the input because it was designed for use with portable players which are generally under 1 volt. Sometimes the input overload point may depend on the gain settings. So check the documentation for a given amp--especially if you plan to use home sources with a portable amp, or sources with more than 2 volts of output.
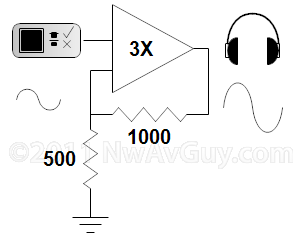 RESISTOR VALUES: Some amplifiers let you set the gain by changing resistor values. The diagram to the right shows a typical non-inverting amplifier stage. The gain is given by 1 + 1000/500 = 3. For all the math, see Wikipedia Gain and Wikipedia Amplifiers. Some amplifiers may have multiple gain stages, in which case you have to multiply the gain of each stage together. So an amp with a 2X and 3X stage has a total gain of 6X.
RESISTOR VALUES: Some amplifiers let you set the gain by changing resistor values. The diagram to the right shows a typical non-inverting amplifier stage. The gain is given by 1 + 1000/500 = 3. For all the math, see Wikipedia Gain and Wikipedia Amplifiers. Some amplifiers may have multiple gain stages, in which case you have to multiply the gain of each stage together. So an amp with a 2X and 3X stage has a total gain of 6X.
DIY GAIN MEASUREMENTS: If you have a decent DMM (multimeter) that can measure x.xx volts AC (i.e. 0.01 volt resolution) you can play back a 60hz 0 dBFS sine wave and measure the output of your source in Vrms. You can create the file with Audacity. Ideally the voltage should be measured using a “Y” cable with your source connected to the amplifier. You can then also (carefully so not to cause short circuits) measure the output of your amplifier. Don’t connect your headphone as they could be damaged. And don’t try higher frequencies as most meters are not accurate much above 60 hz. Vout/Vin = Gain
BOTTOM LINE: Gain is important. There's a definite sweet spot for most headphones and sources. The closer an amp comes to having the ideal gain, the better overall performance you will get.